トランスミッションでギア比が大きいとトルクが増幅する物理的仕組みと計算法

車の運動性能を決定するパワートレイン。

その中でも、エンジンとトランスミッションについては、大きな部分を占めています。

この記事では、トランスミッションのギア比が大きいとトルクが増幅される物理的解説と、トランスミッションの偉大さについてのイメージをお伝えします！

ギアの半径とギアの歯数は比例する

まず、一般的に表されているギア比を考える前に、ギアの半径とギアの歯数について考えていきましょう。

図のように、半径$R_1$のギアAと、半径$R_2$のギアBがあり、噛み合って回転していたとします。

この時に、ガタなく綺麗にスムーズに回転するためには、ギアAとギアBのそれぞれのギアの歯の間隔が一定でなければなりません。

また、ギアAとギアBの歯の間隔も等しくなければ、スムーズに回らないでしょう。

したがって、ギアAとギアBは、両方とも同じ間隔で歯があるといえます。

ここで、歯の間隔を$\delta$としましょう。

歯車Aの歯数は、円周の長さが$2\pi R_1$であることから、次の式で表すことができます。

$$\frac{2\pi R_1}{\delta} \tag{1.1}$$

歯車Bの歯数は、円周の長さが$2\pi R_2$であることから、次の式で表すことができます。

$$\frac{2\pi R_2}{\delta} \tag{1.2}$$

この2つの式を比べると、$R_1$と$R_2$以外は同じです。

したがって、ギアの歯数は、ギアの半径に比例することになります。

ここで、ギア比は、ギアBの歯数とギアAの歯数の比のことを言います。

しかし、歯数はギアの半径に比例することから、ギアBとギアAの半径の比と言い換えることもできます。

以下、ギアに働くトルクを見ていきますので、ギア比を半径に置き換えて、本文の記載を行います。

ギア比が大きいとトルクが増幅される物理的原理

では、ギア比が大きいとトルクが増幅される物理的な原理について見ていきましょう。

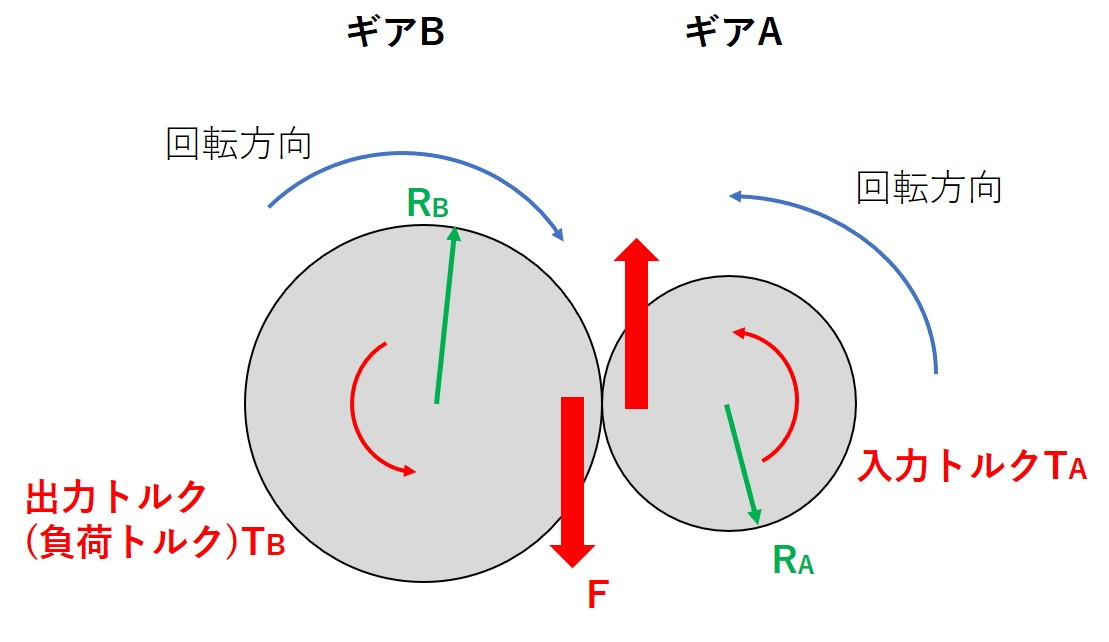
先ほどと同様に、ギアAとギアBが噛み合っていて、ギアAに入力トルク$T_A$を入力したとします。

そして、ギアBには負荷があり、トルク$T_B$を取り出せたとします。

ギアAの回転の運動方程式は、次の式で表すことができます。

$$I_A \frac{d \omega_A}{dt}=T_A-FR_A \tag{2.1}$$

次に、ギアBの回転の運動方程式は、次の式で表すことができます。

$$I_B \frac{d \omega_B}{dt}=FR_B-T_B \tag{2.2}$$

また、ギアの噛み合いから、次の式が成り立ちます。

$$R_A \omega_A=R_B \omega_B \tag{2.3}$$

ここで、計算が面倒になるので、ギアの慣性モーメントを0として無視します。

これにより、これらの3つの式は、次のように簡単化できます。

$$0=T_A-FR_A \tag{2.4}$$

$$0=FR_B-T_B \tag{2.5}$$

$$R_A \omega_A=R_B \omega_B \tag{2.6}$$

1つ目の式と2つ目の式からFを削除します。

すると、次のように計算できます。

$$\frac{T_A}{R_A}=\frac{T_B}{R_B} \tag{2.7}$$

$$T_B=\frac{R_B}{R_A}T_A \tag{2.8}$$

次に、3つ目の式より、$\omega_B$について解くと、

$$\omega_B=\frac{R_A}{R_B}\omega_A \tag{2.9}$$

ギア比として、入力に対する出力の比をAとして、

$$A=\frac{R_B}{R_A} \tag{2.10}$$

を導入すれば、最終的に次の式が得られます。

$$T_B=AT_A \tag{2.11}$$

$$\omega_B=\frac{1}{A}T_A \tag{2.12}$$

この式は、入力トルクはギア比倍されて出力され、回転数は$\frac{1}{ギア比}$倍されて出力されることになります。

トランスミッションで馬力は増幅されない

次に、トランスミッションではトルクは増幅されても、馬力が増幅されないことを見ていきます。

馬力の計算式は、次の式で表されます。

$$馬力=定数×回転数×トルク \tag{3.1}$$

回転数と、角速度は比例するので、上記の馬力の式の定数にこの比例関係を含めることで、次の式になります。

$$馬力=定数×角速度×トルク \tag{3.2}$$

先ほどの問題では、入力側のギアAへのトルクは$T_A$、角速度は$\omega_A$ですので、入力される馬力は次の式になります。

$$入力馬力=定数×\omega_A×T_A \tag{3.3}$$

次に、出力される馬力を計算します。

出力されるトルクは$AT_A$、角速度は$\frac{1}{A}\omega_A$となります。

したがって、出力される馬力を計算すると、次のようになります。

$$出力馬力=定数×\frac{1}{A}\omega_A×AT_A=定数×\omega_A×T_A \tag{3.4}$$

入力馬力と出力馬力は等しくなるので、トランスミッションで馬力の増幅は行われないことがわかりました。

以上の内容で、トランスミッションのギア比によって、トルクはギア比倍に増幅され、回転数は$frac{1}{ギア比}$倍になることがわかりました。

以下の内容は、ギアの慣性モーメントを含めた考察を行っていきます。

慣性モーメントの大きさは損失になりますが、無暗に慣性モーメントを小さくすると、ギアへの負担が大きくなることを導きます。

ギアの慣性モーメントとトランスミッションの伝達効率の関係

次に、ギアの慣性モーメントとトランスミッションの伝達効率の関係について考えていきます。

先ほどの問題では、ギアの慣性モーメントである$I_A$と$I_B$を無視して計算を簡単化していました。

しかし、現実の物体には回転軸を中心とした慣性モーメントがあり、次の式で回転のエネルギーを持ちます。

$$\frac{1}{2}I\omega^2 \tag{4.1}$$

この式から、回転体の回転エネルギーは、慣性モーメントに比例し、また回転数の2乗に比例する形で増加します。

ギアは当然回転していますから、ギアAに入力された馬力の一部は、ギアAとギアBの回転エネルギーとして吸収されます。

入力されるエネルギーを$U_{in}$とし、ギアAの回転エネルギーを$U_A$、ギアBの回転エネルギーを$U_B$、出力されるエネルギーを$U_{out}$とすれば、次の関係式が成立します。

$$U_{out}=U_{in}-U_A-U_B \tag{4.2}$$

$U_A$と$U_B$は、回転エネルギーの式である式(4.1)より、それぞれ次のように表されます。

$$U_A=\frac{1}{2}I_A{\omega_A}^2 \tag{4.3}$$

$$U_B=\frac{1}{2}I_B{\omega_B}^2 \tag{4.4}$$

結果的に、出力されるエネルギーは次の式で表されます。

$$U_{out}=U_{in}-\frac{1}{2}I_A{\omega_A}^2-\frac{1}{2}I_B{\omega_B}^2 \tag{4.5}$$

ここで、$U_{out}$と$U_{in}$は、入力されたエネルギーの総和、つまり時刻0からの馬力の積分値になります。

エンジンの馬力は、その瞬間の単位時間当たりの出力で表されます。

したがって、エンジン馬力$P_{in}$と、出力される馬力$P_{out}$で馬力で換算するためには、$U_{in}$と$U_{out}$を時間で微分したものである、

$$P_{in}=\frac{dU_{in}}{dt} \tag{4.6}$$

$$P_{out}=\frac{dU_{out}}{dt} \tag{4.7}$$

の関係を用います。

$P_{in}$と$P_{out}$は、時系列におけるエネルギー総和の瞬間的な変化量を示しています。

したがって、これが馬力（=出力[kW）になります。

式(4.5)に、式(4.6)と式(4.7)の関係を適用するために、式(4.5)の両辺を微分し、式(4.8)のようにします。

$$\frac{U_{out}}{dt}=\frac{U_{in}}{dt}-I_A\omega_A\frac{d\omega_A}{dt}-I_B\omega_B \frac{d\omega_B}{dt} \tag{4.8}$$

したがって、慣性モーメントの値に対して、速度と加速度に比例する形で損失が生じています。

具体的には、$\omega_A$と$\omega_B$が大きい高速走行時から、速度変化の大きさを示す$\frac{d\omega_A}{dt}$と$\frac{d\omega_B}{dt}$が大きくなるような、すなわち急激な加速を行うときに損失が大きくなります。

したがって、慣性モーメントが小さい方が、トランスミッションにおける変換効率が高いことがわかります。

トルクの増幅について見ていくと、入力される馬力$P_{in}$と出力される馬力$P_{out}$は、次の式で表されます。

$$P_{in}=C×\omega_A×T_A \tag{4.9}$$

$$P_{out}=C×\omega_B×T_B \tag{4.10}$$

ここで、$C$は式(4.9)と式(4.10)で共通の定数です。

式(4.8)、式(4.9)、式(4.10)より、式(4.11)になります。

$$C\omega_B T_B=C\omega_AT_A-I_A\omega_A\frac{d\omega_A}{dt}-I_B\omega_B \frac{d\omega_B}{dt} \tag{4.11}$$

$T_B$について解きます。

$$T_B=\frac{\omega_A}{\omega_B}T_A-\frac{I_A\omega_A}{C\omega_B}\frac{d\omega_A}{dt}-\frac{I_B}{C} \frac{d\omega_B}{dt} \tag{4.12}$$

回転数の比の式である式(2.12)より、$\frac{\omega_A}{\omega_B}=A$で置き換えて、式(4.13)を得ます。

$$T_B=AT_A-\frac{I_A A}{C}\frac{d\omega_A}{dt}-\frac{I_B}{C} \frac{d\omega_B}{dt} \tag{4.13}$$

式(4.13)を見ると、右辺第二項と第三項は$I_A=0$、$I_B=0$の条件下では0となり、慣性モーメントを無視した式である式(2.8)と一致します。

したがって、出力トルクの低下を招く式(4.13)の右辺第二項と第三項は損失となり、きれいにトルクはギア比倍されません。

トルクの観点から見ても、ギアの慣性モーメントは、できるだけ小さいほうがいいことになります。

ギアの慣性モーメントと歯車への負担

慣性モーメントを小さくするには、回転中心から遠い場所に重量物を配置しないことで小さくすることができます。

ギアを質量M、半径Rの一様な円盤として見た場合、近似的な慣性モーメントは、式(5.1)で示されるものになります。

$$I=\frac{1}{2}MR^2 \tag{5.1}$$

したがって、慣性モーメントを小さくする一番早い方法として、ギアの半径Rを小さくする方法があります。

しかし、この場合にはギアの歯の部分の負荷が増大してしまいます。

先の章で示した、慣性モーメントを無視していない式を再度見てみます。

$$I_A \frac{d \omega_A}{dt}=T_A-FR_A \tag{5.2}$$

$$I_B \frac{d \omega_B}{dt}=FR_B-T_B \tag{5.3}$$

$$R_A \omega_A=R_B \omega_B \tag{5.4}$$

式(5.4)より、$\omega_B$について解くと、次の式になります。

$$\omega_B=\frac{R_A}{R_B}\omega_A \tag{5.5}$$

この式を、式(5.3)に代入します。

$$I_B \frac{R_A}{R_B}\frac{d \omega_A}{dt}=FR_B-T_B \tag{5.6}$$

式(5.6)を、$\frac{d\omega_A}{dt}$について解きます。

$$\frac{d \omega_A}{dt}=\frac{R_B}{I_BR_A}(FR_B-T_B) \tag{5.7}$$

式(5.2)を、$\frac{d\omega_A}{dt}$について解きます。

$$\frac{d\omega_A}{dt}=\frac{1}{I_A}(T_A-FR_A) \tag{5.8}$$

式(5.7)と式(5.8)から、$\frac{d \omega_A}{dt}$を消去し整理すると、次の式になります。

$$\frac{R_B}{I_BR_A}(FR_B-T_B)=\frac{1}{I_A}(T_A-FR_A) \tag{5.9}$$

$$(\frac{{R_B}^2}{I_BR_A}+\frac{R_A}{I_A})F=\frac{R_B}{I_BR_A}T_B+\frac{1}{I_A}T_A \tag{5.10}$$

$$F=\frac{\frac{R_B}{I_BR_A}T_B+\frac{1}{I_A}T_A}{\frac{{R_B}^2}{I_BR_A}+\frac{R_A}{I_A}} \tag{5.11}$$

ギアを一様な円盤とした近似的な慣性モーメントである式(5.1)を適用します。

$$F=\frac{\frac{2}{M_BR_AR_B}T_B+\frac{2}{M_A{R_A}^2}T_A}{\frac{2}{M_BR_A}+\frac{2}{M_AR_A}} \tag{5.12}$$

$$F=\frac{\frac{M_A}{R_B}T_B+\frac{M_B}{R_A}T_A}{M_A+M_B} \tag{5.13}$$

ここで、ギアの密度を$\rho$として、ギアAとギアBの質量$M_A$と$M_B$をそれぞれ次のように表します。

$$M_A=\rho \pi{R_A}^2 \tag{5.14}$$

$$M_B=\rho \pi {R_B}^2 \tag{5.15}$$

すると、

$$F=\frac{\frac{\rho\pi{R_A}^2}{R_B}T_B+\frac{\rho\pi{R_B}^2}{R_A}T_A}{\rho \pi{R_A}^2+\rho \pi {R_B}^2} \tag{5.16}$$

さらに、ギア比を固定すれば、
$A=\frac{R_B}{R_A}$
より、
$R_B=AR_A$となるので、

$$F=\frac{\frac{\rho\pi{R_A}^2}{AR_A}T_B+\frac{\rho\pi A^2{R_A}^2}{R_A}T_A}{\rho \pi{R_A}^2+\rho \pi A^2{R_A}^2} \tag{5.17}$$

すなわち、

$$F=\frac{1}{R_A}\frac{\frac{1}{A}T_B+A^2 T_A}{1+A^2} \tag{5.18}$$

式(5.18)より、ギア比Aと入力トルク$T_A$、出力トルク$T_B$が同じ条件であれば、ギアAの半径$R_A$に反比例する形で、ギアの歯に加わる力が増大します。

見やすくなるように、慣性モーメントの影響による損失がなく、理想的なトルク増幅が得られると仮定すれば、$T_B=AT_A$となるので、

$$F=\frac{1}{R_A}\frac{1+A^2}{1+A^2}T_A=\frac{1}{R_A}T_A \tag{5.19}$$

したがって、あるギア比Aを実現するために、入力側ギアの半径を$R_A$とすれば、ギアを構成する歯に加わる力は、入力ギアの半径$R_A$に反比例することがわかります。

一般的な反比例のグラフである、$y=\frac{1}{x}$は下のグラフのようなものです。

したがって、ある領域までは$R_A$の変化に伴う歯への負荷の増大量はわずかですが、ある半径$R_{A0}$を境目に、急激に負荷が増大します。

これより、トランスミッションのギアにおける伝達効率は、ギアの慣性モーメントが大きいほど悪くなります。

慣性モーメントを小さくするためには入力ギアと出力ギアのギア比を一定に保ったままその半径を小さくする必要があります。

しかし、小さくしすぎるとギアの歯に加わる力が反比例にしたがって増大するため、無暗にギアの半径$R_A$を小さくすることはできません。

どこまでの効率を求めるか、さらにはどこまでの耐久を持たせるかのトレードオフの関係になる部分なので、深く考えれば面白い部分です。

まとめ

ここまで、ギア比でトルクが増大されることについて物理的な説明を行ってきました。

結論として分かったことを、再度ここでまとめておきます。

ギアの慣性モーメントを無視した式から、トルクはギア比倍される。

→式(2.11)

また、歯車の噛み合いの式から、回転速度は$\frac{1}{ギア比}$になる。

→式(2.12)

慣性モーメントが大きいと、伝達効率が悪くなる。

→式(4.5)

ギアの慣性モーメントが大きい場合、トルクはギア比倍されない。

→式(4.10)

慣性モーメントを小さくするには、入力と出力のギア比を保ったまま、ギアの半径を小さくすることが有効です。

→式(5.1)

その場合、トランスミッションの伝達効率は増大しますが、ギアへの負担が大きくなります。

→式(5.19)

トランスミッションのギア比によって、トルクが増大されるというテーマで記事を書いてきましたが、ギアの噛み合いだけでもいろいろと考えることのできる部分があります。

今後は、こうした記事も投稿していけたらと思っています。