
ホンダ渾身のシビックタイプRとスバルの象徴WRX STI。
320PSのハイパワーのFFと、308PSの安定性のAWD。
エンジン性能に着目して、加速性能を比較してみました。
今回はMT車ということで、AT車にはないクラッチミートの瞬間までを考慮します。
内容が多く、かなり長編の傑作になりますが、少しずつ解明していきましょう。
目次
シビックタイプRとWRX STIの基本情報
シビックタイプR
直列エンジン4気筒2.0Lターボ
最高出力:235kW(320PS)/6500rpm
最大トルク:400Nm(40.8kgf・m)/2500-4500rpm
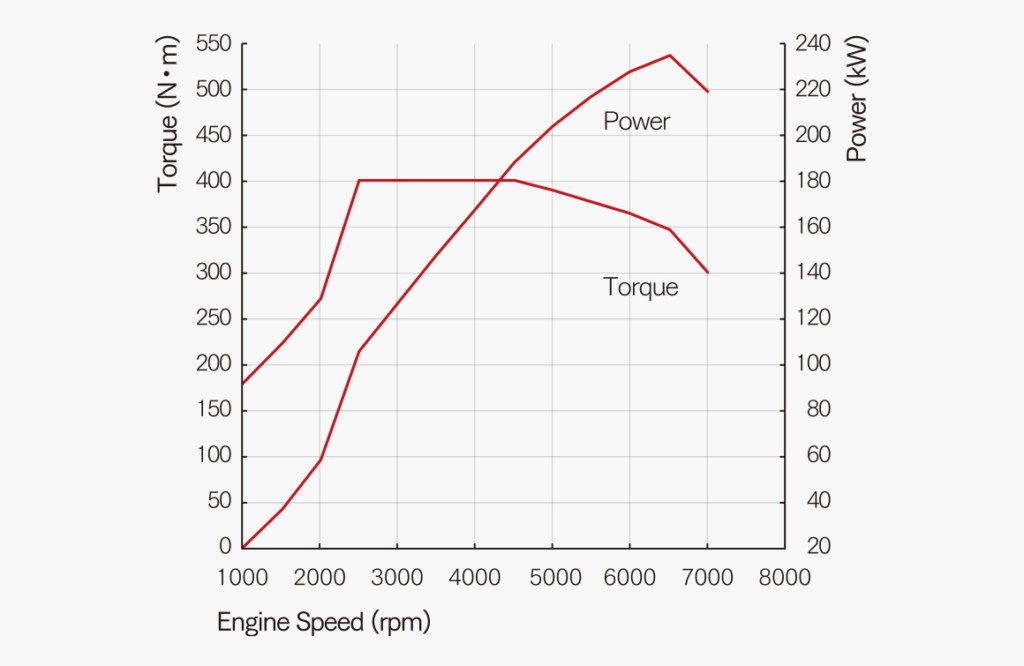
減速比については以下の通りです。
1速:3.625
2速:2.115
3速:1.529
4速:1.125
5速:0.911
6速:0.734
最終:4.111

WRX STI
水平対向4気筒2.0Lターボ
最高出力:237kW(308PS)/6400rpm
最大トルク:422Nm(43.0kgf・m)/4400rpm
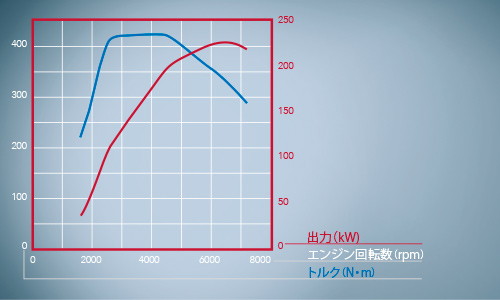
減速比については以下の通りです。
1速:3.636
2速:2.375
3速:1.761
4速:1.346
5速:1.062
6速:0.842
最終:3.900

加速性能は馬力で決定される?
今までこのブログでは、「加速性能は馬力のみで決定される。」と言ってきましたが、MT車のクラッチミートの瞬間まで考えるとなかなか話が複雑化してきます。
まずは、なぜ馬力で決定されるのか?という点について考えてみます。

加速性能は、クラッチ部分伝達効率を無視すれば馬力で一意に決まる。
タイヤに伝わるトルクは、エンジン発生トルクがトランスミッションで増幅されて、タイヤに伝わります。

エンジンから始まり、トランスミッションを経てタイヤまで伝達されていくトルクは、次の式で表せます。
$
伝達トルク=エンジン発生トルク×減速比
$
ここで、減速比は次の式で置き換えることができます。
$減速比=\frac{エンジン回転数}{トランスミッション出力回転数}$
そして、タイヤに伝達するまでの最終減速比まで考慮に入れると、
パワートレイン全体の減速比は、次の式で表すことができます。
$
全体の減速比=\frac{エンジン回転数}{タイヤ回転数}
$
したがって、タイヤに伝わるトルクは、次の式で表すことができます。
$
エンジン発生トルク×\frac{エンジン回転数}{タイヤ回転数}
$
ここで、エンジン発生トルク×エンジン回転数は馬力であるため、タイヤへの伝達トルクは次の式で表すことができます。
$
タイヤへの伝達トルク=\frac{エンジン出力}{タイヤ回転数}
$
タイヤ回転数は、車速により決定されるため、最高出力を維持しながら加速することで、その車速に応じた最大加速力で加速できることになります。
だからCVTは最高出力発生回転数一定で加速するのです。
この議論そのものは全く間違いじゃなんです。

でも、MTの場合には、クラッチでの滑りまで状況に入ってくるのです。
0-100加速などは、エンジン回転数をレブリミットまで回してから、
強引に加速しますよね?
1速で、クリープぐらいの速度でクラッチが100%つながった状態で加速する人はいないでしょう。
この部分がややこしいのです。
逆に、ターボラグは考慮しなくても大丈夫ですね。
エンジンを振り回した状態でスタートするのですから、
AT車のようにターボラグなんてありません。
今回は、クラッチミートの瞬間までを考慮して、シビックタイプRとWRX STIの加速性能を比較します。
エネルギ-保存則
エネルギー保存則をご存知でしょうか?
エネルギーは、絶対に保存されることですね。
エンジンから発生した馬力(エネルギー)は、AT車の場合は一定効率でタイヤに伝達されますが、
MTの場合はクラッチ操作で可変です。
タイヤに伝達されなかったエネルギーは、摩擦熱として捨てられます。
クラッチの圧着力をF、動摩擦係数をuすると、次の式で表されます。
$摩擦力=\frac{F}{u}$
ここで、滑りを定義します。
$すべり=\frac{クラッチ出力回転数}{エンジン回転数}$
つまり、エンジンパワーのどれぐらいが加速に使われたかを示す値になります。
逆に、$1-すべり$は、どれだけが摩擦熱になったかという損失を表します。
滑りの物理的な意味
ここで、すべりを定義した物理的な意味を考えます。
そのために、クラッチ部分におけるエネルギーの伝達を詳しく見ていきましょう。
まずは、クラッチを半径Rの円盤と考えます。
エネルギー保存則は、発生したエネルギーは、消滅しないことを表します。
つまり、エンジンから発生したエネルギーは、考えている物理空間の中で必ず保存されています。
クラッチのみの損失を考慮したばあい、エンジン発生馬力は、タイヤまで伝わるエネルギーと、クラッチでの摩擦による熱エネルギーに変換されます。
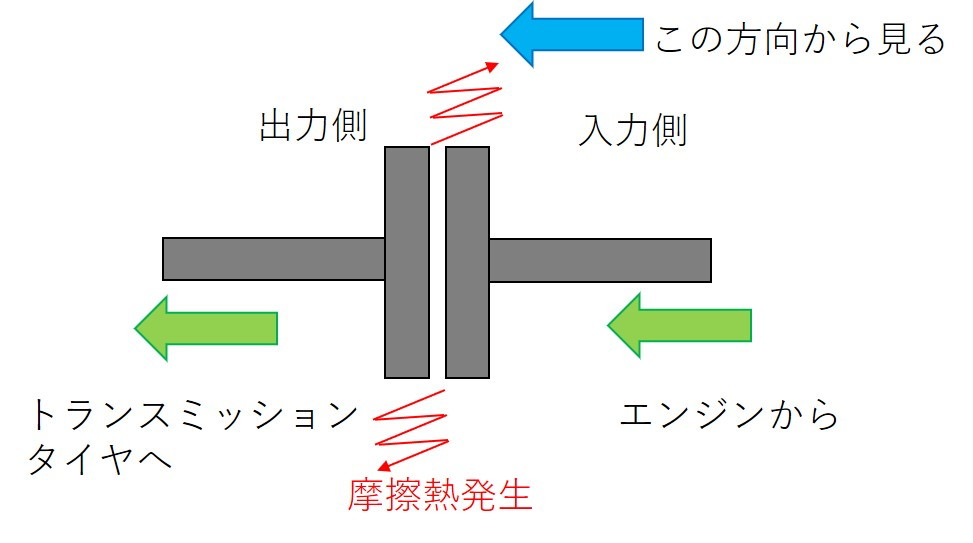
つまり、エンジン発生出力から、摩擦損失を引けば、タイヤまで伝わるエネルギーになります。
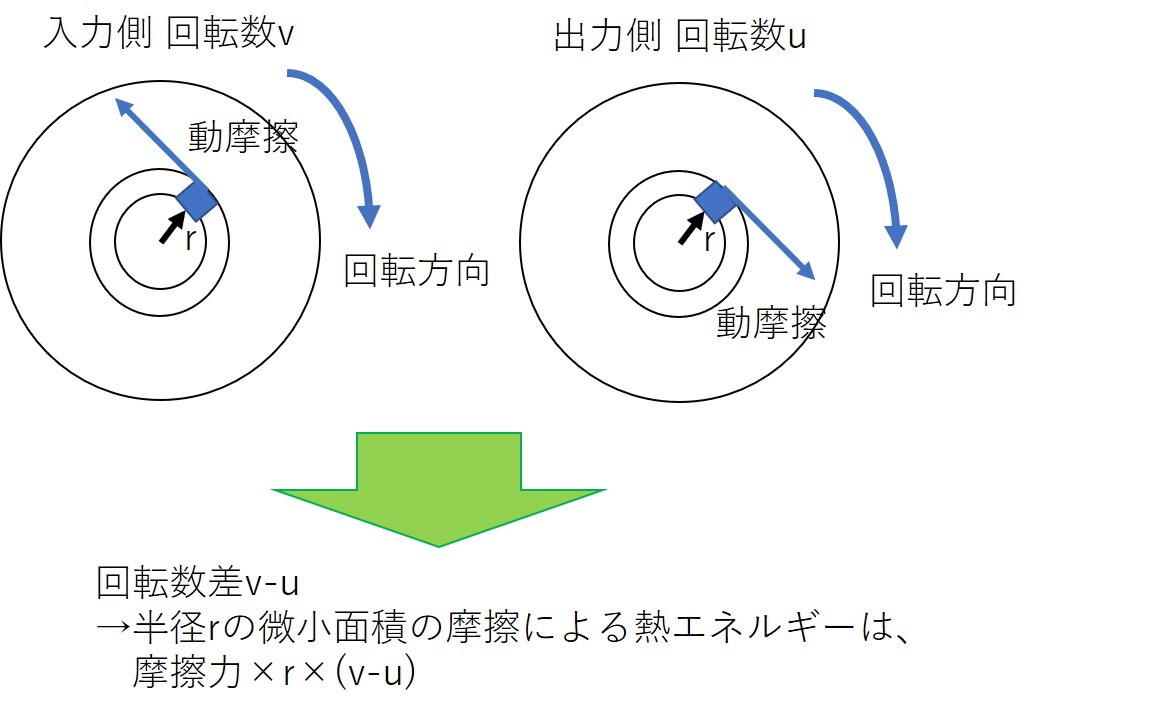
クラッチ入力回転数(=エンジン回転数)を$v$とし、
クラッチ出力回転数を$u$とします。
この時、相対的な回転速度差は$v-u$です。
クラッチの圧着力(摩擦力を考えるときの垂直抗力)をFとし、
動摩擦係数をμとします。
この時、クラッチ面積$S$とすれば、単位面積当たりの摩擦力は、次の式で表すことができます。
$摩擦力=\mu\frac{F}{S}$
半径rの位置における単位時間当たり、微小面積$dS$の摩擦による熱エネルギーは、次のようになります。
$\delta U=\mu \frac{F}{S}r(v-u)dS$
これを、クラッチ全体で積分することで、単位時間当たりの熱エネルギー損失がわかります。
$
U=\int_S \mu \frac{F}{S}r(v-u)dS \\
=\int_0^R \mu \frac{F}{S}r(v-u)2\pi r dr \\
=2\pi \mu \frac{F}{S}(v-u)\frac{R^3}{3}
$
ここで、$S=\pi R^2$であることより、次のようになる。
$U=2\mu \frac{F(v-u)R}{3}$
そして、エンジン出力から引くことで、タイヤへの伝達エネルギーがわかります。
$タイヤへの伝達エネルギー=P-U\\
=P-2\mu \frac{F(v-u)R}{3}$
出力側クラッチから見る
次に、出力側クラッチを基準に見てみます。
出力側クラッチは、クラッチ面による動摩擦で駆動します。
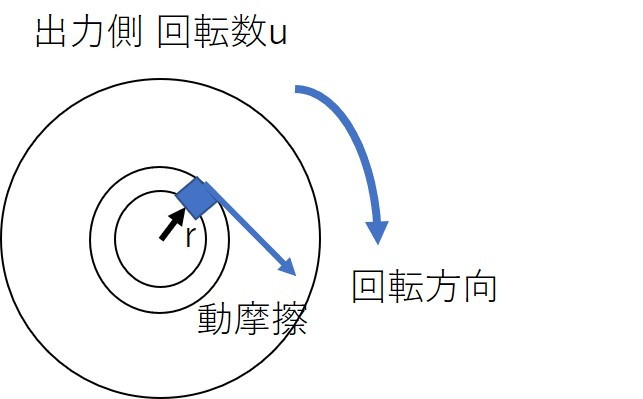
まずは、出力側クラッチに働く摩擦力によるトルクを考えると、
微小面積$dS$に働く摩擦力によるトルクは、次の式になります。
$t_c=\mu \frac{F}{S}r dS$
これを、クラッチ面全体で積分します。
$
T_c=\int_S t_c dS \\
=\int_S \mu \frac{F}{S}r dS \\
=\int_0^R \mu \frac{F}{S}r 2\pi r dr \\
=2 \pi \mu \frac{F}{S}\frac{R^3}{3}
$
ここで、$S=\pi R^2$より、
$
T_c=\mu \frac{FR}{3}
$
出力=トルク×回転数なので、
出力側クラッチの回転数uをかけることで、
クラッチ通過後の出力がわかり、以下のものになります。
$
クラッチの伝達エネルギー=\mu \frac{FuR}{3}
$
2つの式を比較する。
エネルギー保存より導かれた式
$P-\mu \frac{F(v-u)R}{3}$
クラッチ出力側を基準にトルクから導かれた式
$
\mu \frac{FuR}{3}
$
この2つの式は、導き方は違いますが、求めているものはタイヤへの伝達エネルギーであり、等しくないといけません。
そこで、エネルギー保存から求められた式を、次のように変形してみます。
$
P-\mu \frac{F(v-u)R}{3}\\
=P-\mu (\frac{FvR}{3}-\frac{FuR}{3})\\
=P-\mu \frac{FvR}{3}+\mu \frac{FuR}{3}
$
つまり、次の関係が成り立てばいいです。
$
P=\mu \frac{FvR}{3}
$
これは、エンジン発生エネルギーが、$\mu \frac{FvR}{3}$で与えられることを表しています。
本当に正しいのか、物理的に考えてみます。
エンジン出力エネルギーを100%伝達時の伝達エネルギーで考える。
前の節で、エンジン発生エネルギーが、次の式で表せるのではないか?
と考えました。
$P=\mu \frac{FvR}{3}$
これが本当に正しいのかを考えます。
例えば、クラッチが100%滑りなしで駆動した場合、
クラッチ出力側のエネルギーは、
クラッチ出力側を基準にトルクから導かれた式
$
クラッチの伝達エネルギー=\mu \frac{FuR}{3}
$
において、$u$を$v$で置き換えればよく、次の式で表せます。
$\mu \frac{FvR}{3}$
これが伝達効率100%の出力で、エンジン発生エネルギーを100%タイヤに伝えている状態です。
比べると、先ほど挙げた式と同じですね。
つまり、伝達効率100%で伝達した時の伝達エネルギーなので、
$\mu \frac{FvR}{3}$
はエンジン出力と同等ということがわかりますね。
つまり、エンジン出力は、
$P=\mu \frac{FvR}{3}$
と表すことができます。

エンジン出力エネルギーを熱エネルギーで考える。
また、出力側回転数が0の場合、100%摩擦熱になりますが、摩擦熱は、先ほど求めた摩擦熱の式、
$U=\mu \frac{F(v-u)R}{3}$
において、$u=0$とすると、次のようになります。
$U=\mu \frac{FvR}{3}$
これは、クラッチにおいて全くエネルギーが伝達されず、
エンジン出力のすべてが摩擦熱になっていることを表します。
すなわち、ここで生じた摩擦熱は、エンジン出力そのもでのす。
これより、エンジン出力は、クラッチ側の圧着力$F$、クラッチ入力側の回転速度$v$、動摩擦係数$\mu$を用いて、次のように表せることがわかります。
$P=\mu \frac{FvR}{3}$
すべりを定義する。
これがわかると、滑りが定義できます。
$
タイヤへの伝達エネルギー \\
=\mu \frac{FuR}{3}\\
=\frac{\mu \frac{FuR}{3}}{P} P \\
=\frac{ \mu \frac {FuR}{3} } {\mu \frac{FvR}{3}}P \\
=\frac{u}{v}P\\
=すべり×エンジン出力
$
これが、先ほど説明した、「すべり」の意味になります。

滑りを考慮すると、トルク曲線が見えてくる。
先ほど定義した滑り、エンジン出力にかけてみましょうか。
タイヤへの伝達馬力=エンジン発生馬力×滑り
=エンジン発生トルク×エンジン回転数×クラッチ出力回転数÷エンジン回転数
=エンジン発生トルク×クラッチ出力回転数
となり、トルクが全面的に出てくるのです。
つまり、シビックタイプRも、WRX STIも、停車状態でクラッチミートした場合、
エンジン回転数は、最大トルク発生系点数になるのが理想です。
つまり、レブリミットまで回すだけ回していて、
一気に半クラッチでつないだ瞬間に、最大トルク発生回転数を維持するのが理想です。
いつになったらエンジン回転数を上げるか?
トルクなのか、出力なのかややこしくなってきてますが、
最大トルクが重要なのか、最高出力が重要なのかの境目は、
滑りが0になった瞬間なのです。
つまり、クラッチが完全につながっ時、
もっと言えば、クラッチ出力回転数が、エンジンの最大トルク発生回転数と同期した瞬間からは、
最高出力が生きてきます。
ややこしいので、タイプRの場合で具体的に見ていきましょう。
タイプRのエンジン性能は、
最高出力:235kW(320PS)/6500rpm
最大トルク:400Nm(40.8kgf・m)/2500-4500rpm
となっていて、エンジン性能曲線は次の図になります。

クラッチの出力回転数が1rpmの時
さすがに0rpmではエンストしてしまうので、
1rpmとしてみてみましょう
エンジンの出力曲線に対して、
エンジン出力×滑り
すなわち、
エンジン出力×1÷エンジン回転数
のグラフが次のようになります。
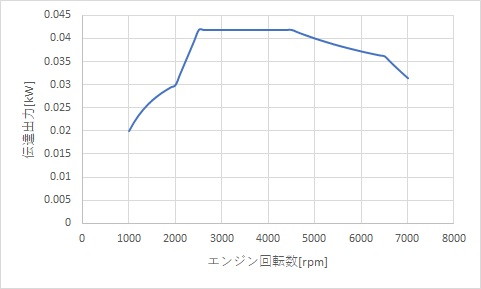
グラフを見てもわかるように、最大トルク発生回転数が見事に反映されいます。
つまり、レブリミットまで回し切った後のクラッチミ-トの瞬間に、エンジン回転数が2500-4500rpmの間に収まるような繊細なクラッチ操作が必要になります。
クラッチの出力回転数が500rpmの時
次に、もう少し加速して、
クラッチ出力回転数が500rpmの場合を見てみましょう。
計算方法は同じです。
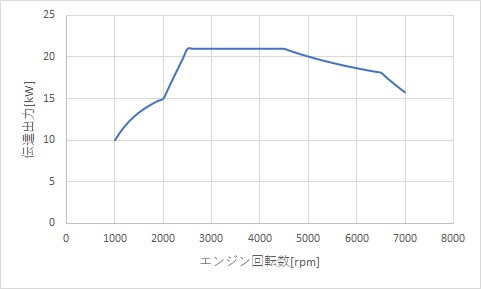
やはり、最大トルク回転数2500-4500rpmでの加速が最も良いことになりますね。
クラッチの出力回転数が4500rpmの時
では、クラッチ出力回転数が4500rpmになったときはどうでしょうか?
計算方法が同じですが、注意が必要です。
滑りをクラッチ出力回転数÷エンジン回転数と定義したので、
滑りは必ず1以下でないとだめです。
もし滑りが1以上なら、それはエンジンよりもクラッチが高速回転していることになり、条件的に適しません。
つまり、4500rpmの時点では、4500rpm未満のエンジン回転数は適さない答えとなります。
そこで、4500rpm以上の回転数のみでグラフを描くと次のようになります。
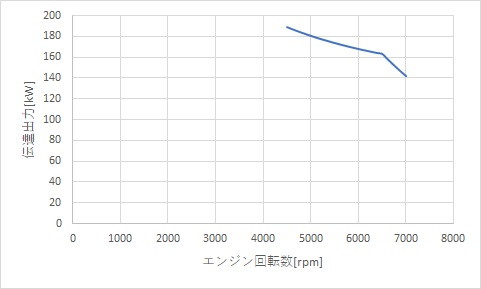
この時点でも、やはり最大トルク発生回転数が効いてきます。
クラッチの出力回転数が6000rpmの時
最後に確認で、6000rpmの時も考えます。
4500rpmの時の結果と同じように、6000rpm以降のみが条件的に適する範囲となります。
今までの最適解は、最大トルク発生回転数でしたが、今回考える6000rpmは、もう、最大トルク発生回転数は超えています。
するとどうなるでしょうか?
その時のグラフは次のようになります。
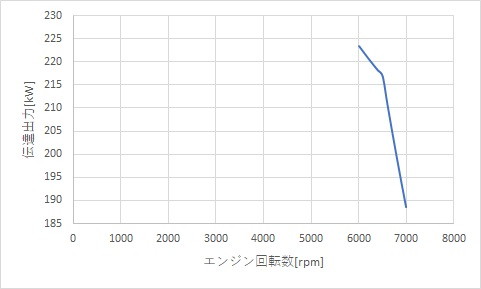
グラフからわかるように、6000rpmという答えが見えます。
つまり、滑りは0ですね。
最大トルク発生回転数を越えれば、滑らさずに加速するほうが加速性能はよくなります。
MT車の最大加速力
今までの考察をすべてまとめると、
クラッチ出力回転数が、最大トルク発生回転数以下であれば、
最大トルク発生回転数で滑らせながら加速する。
一方で、クラッチ出力回転数が、
エンジン最大トルク発生回転数に追い付くと、
滑らさずに加速させていくことがいいとわかります。
言い換えれば、滑りがないということは、AT車と同じで、
馬力曲線によって加速力が決定されます。
これにより、MT車特有のクラッチの滑りを考慮した加速性能の検討が行えるようになりました。
なお、最高速に関しては、馬力で決定されます。
最高速の話なので、
クラッチ出力回転数は、最大トルク発生回転数を優に超えます。
よって、最高出力発生回転数が最高速になります。
MT車の加速性能比較の要点
結局のところ、MT車の加速性能を比較するには、
クラッチ滑りありの領域では、最大トルク。
滑りなしでは出力曲線に従います。
もっとまとめると、
MT車の加速性能の指標は、
最大トルクと、最大トルク以降の出力曲線
で決定されるといえますね。

シビックタイプRとWRX STIのエンジン特性の比較
ここでざっくりとした比較を行うと、
最大トルクではWRX STIが有利。
最大トルク発生回転数以降の出力曲線はタイプRが有利です。
つまり、WRX STIは瞬発力があります。
シビックタイプRは伸びがあります。
シビックタイプRの車速と最高加速力の曲線
クラッチの滑りを考慮したシビックタイプRの最高加速力曲線です。
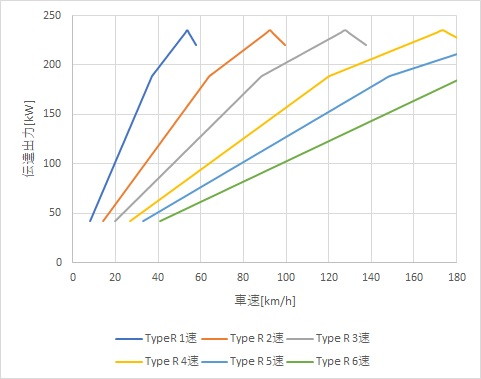
WRX STIの車速と最高加速力の曲線
クラッチの滑りを考慮したWRX STIの最高加速力曲線です。
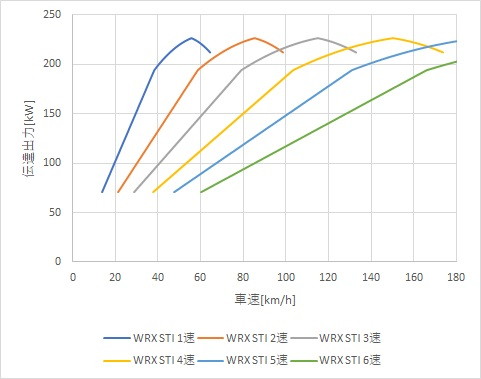
シビックタイプRとWRX STIの加速性能比較
先ほどのシビックタイプRとWRX STIの最高加速を発揮する性能曲線を重ねて比較します。
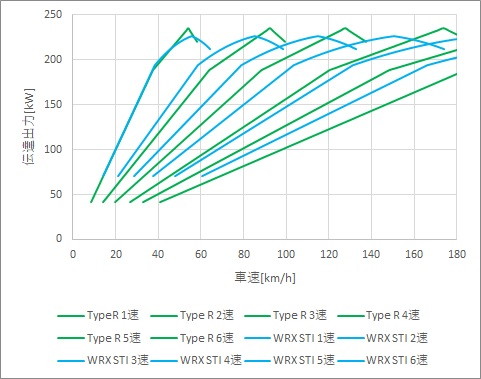
まずわかることは、低速域ではWRX STIの方が、出力のつながりがいいことです。
つながりがいいということは、1速→2速にシフトアップしても、加速力が連続的につながり、急激に加速が落ちることがありません。
一方で、シビック タイプRでは、1速と2速の加速力の開きが大きく、シフトアップ後には大きく駆動力が下がってしまいます。
加速力は、ピーク加速こそシビック タイプRが上回りますが、大体の速度でWRX STIの加速力が上回り、WRX STIの方が加速性能がいいと見れます。
では、高速域での加速性能はどうでしょうか?
シビックタイプRとWRX STIの高速域での加速性能比較
先ほどの比較では、180km/hまでで比較しましたが、次に最高速までの加速性能で比較しましょう。
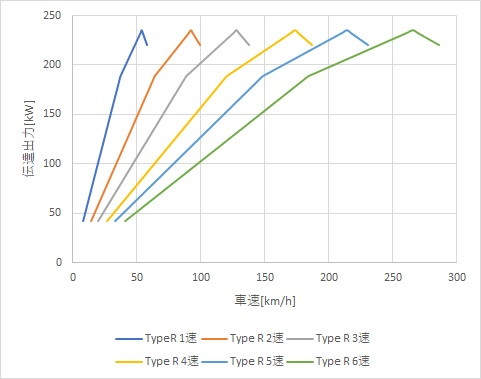
まずは、シビック タイプRです。
見てわかるように、4速以降の加速力のつながりが良くなってきます。
この速度域に来てこそ、シビック タイプRの真価が発揮されるといえます。
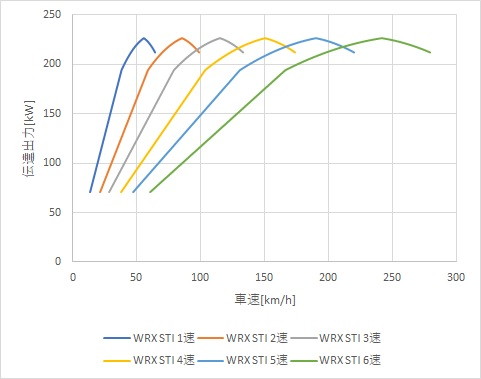
次に、WRX STIです。
重ねて比較します。
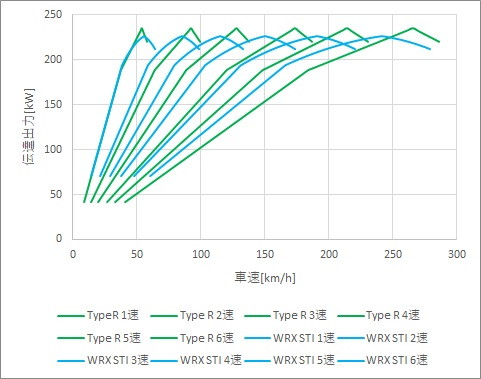
分かることは、150km/hを越えたあたりから、シビック タイプRの加速力が上回っています。
WRX STIはローギアといわれますが、その理由はこのことを意味していることが分かります。
まとめ
シビック タイプRとWRX STIの加速性能を比較してきました。

その中で、まずはMT車の加速性能の比較方法を考え、シビック タイプRとWRX STIの最大加速性能の比較を行いました。
最後に、最高速までの加速性能を比較し、シビック タイプRは約150km/hを越えてから性能が最大限発揮されるような設計になっていることがわかりました。