
スバル独自開発のトランスミッションである、リニアトロニック。
リニアトロニックを含むCVTのメリットは、エンジンの効率のいい回転数を維持できること。
しかし、ここで疑問が!
S#モードでは、8速ステップ制御になるではないか!
この理由を、リニアトロニックに働く力から、伝達効率の面で考察してみました。
目次
チェーンに働く力の分類
リニアトロニックは、チェーン式CVTです。
入力側プーリー、出力側プーリーに挟まれた、駆動力伝達チェーンによって、動力伝達が行われます。
また、入力側プーリー、出力側プーリーのそれぞれの巻きかけ径を変化させることで、無段階変速を行います。
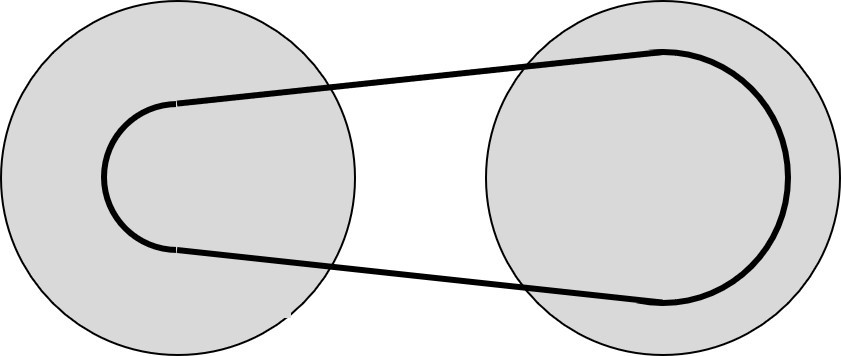
リニアトロニックにおける力を考えるうえで、このチェーンに働く力は2種類の方向に分類できます。
円周方向の力
円周方向の力は、主に駆動力の伝達により働く力です。
エンジンからの駆動力が入力されると、チェーンは引っ張られて回転することは想像できると思います。
これは、入力プーリーにトルクが加わることで、チェーン全体に円周方向の力が働いて、全体として回転方向の運動が生じていることになります。
半径方向の力
半径方向の力は、リニアトロニックの変速の際に加わる力です。
チェーンにおける駒の一つ一つを考えると、CVTの変速によって巻きかけ径の変化により半径方向に移動します。
この移動自体が、半径方向に力が生じている証拠となります。
リニアトロニックのコマ一つ一つに働く力をすべて考慮すると、並大抵の計算力では計算できません。
したがって、この記事では、物理的に妥当と思える近似を導入することで、リニアトロニックの動作を解明していきます。

円周方向に働く力
円周方向に働く力は、駆動力による力であると書きました。
しかし、リニアトロニックの動作を考えるうえでは、この円周方向の力は基本的に無視して大丈夫でしょう。
その理由について、ここで書いていきます。
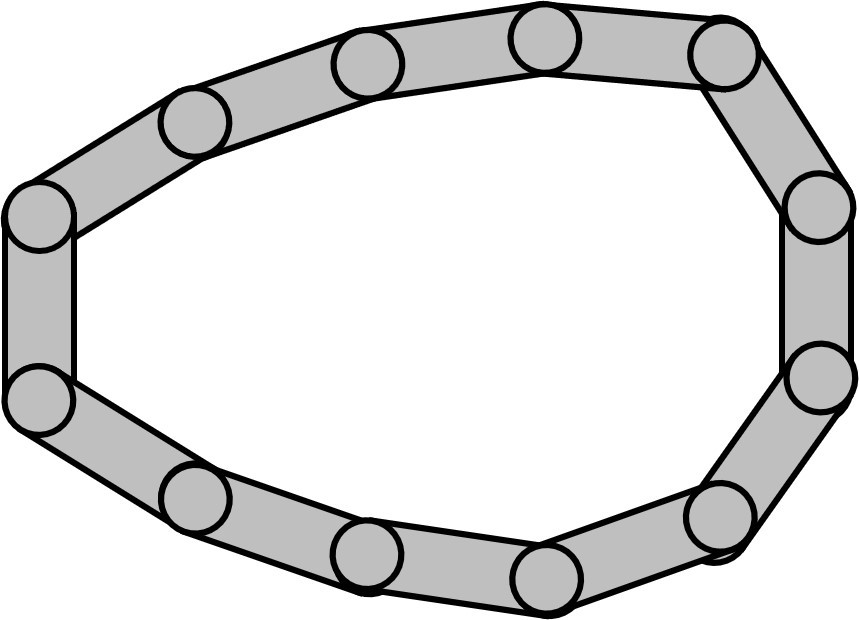
一部三角関数などを使って力の成分分解を行いますが、直感的に分かりやすいように図もたくさん作りました。
まず、円周方向の力は図のように働いています。
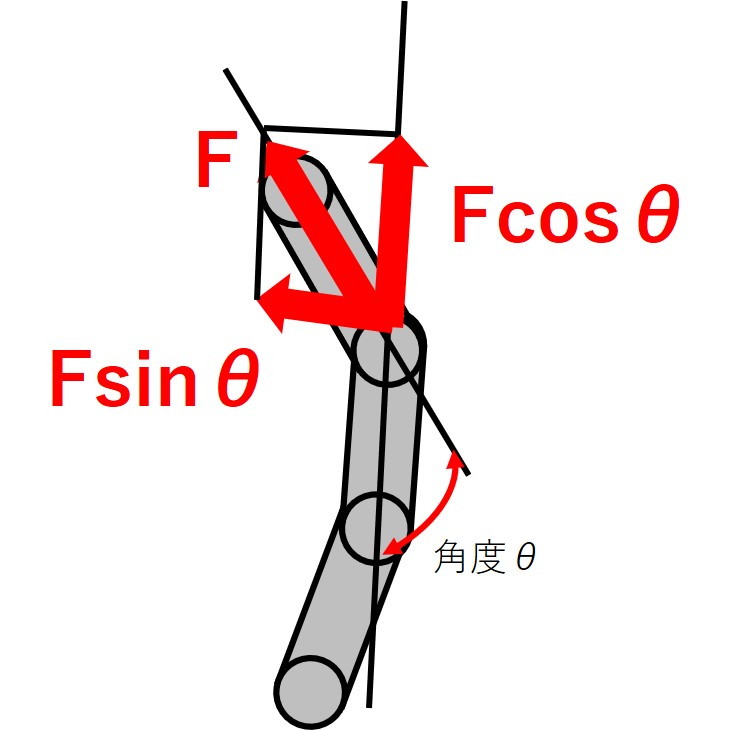
ここで、この図のまま考えた場合には、力の成分分解は上図のように、円周方向の力は半径方向の力の一部にも影響があることになります。
これでは考えにくいので、仮定として、プーリーへの巻きかけ径に対して、チェーンを構成する一つ一つのコマが十分小さいとしましょう。
この仮定自体は問題がないですよね。
コマが大きかったらリニアトロニックを構成できませんから。
この仮定を適用すると、チェーンを構成する駒同士の角度が、限りなく0に近づくことになります。
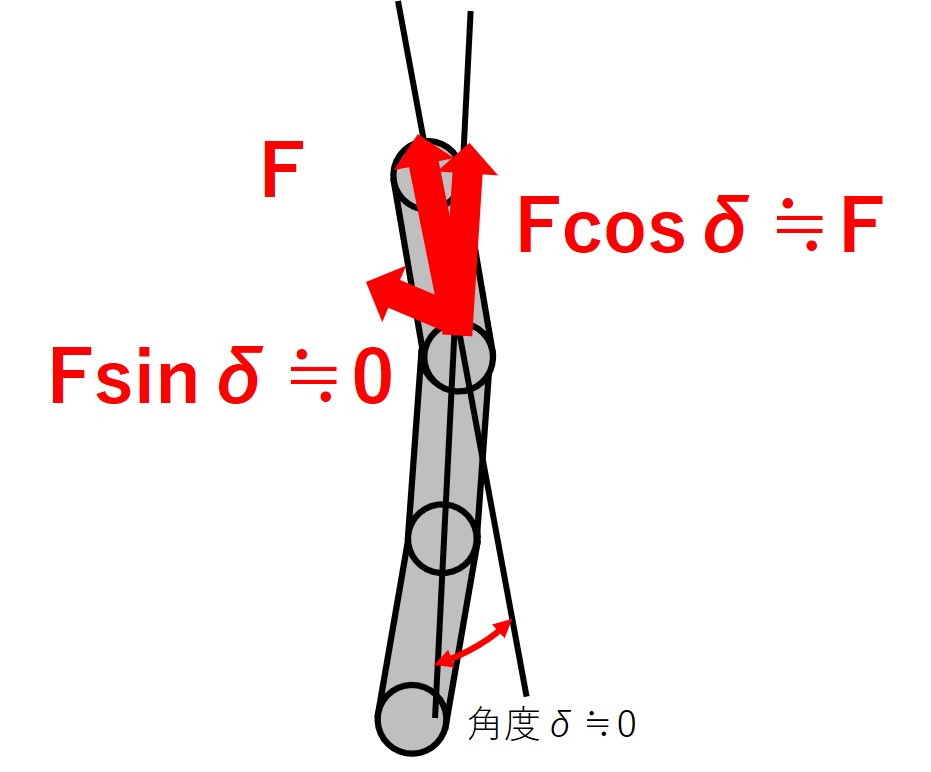
この時、チェーンを構成する駒同士の角度を非常に小さい値$\delta$とします。
こうなると、三角関数において、次の関係式が成り立ちます。
$$cos\delta \fallingdotseq 1$$
$$sin\delta \fallingdotseq 0$$
これによって、円周方向の力を半径方向の軸と、それに直交する座標系で成分分解した場合には、半径方向の成分は0となることがわかります。
これは、チェーンの駆動力の伝達が、リニアトロニックの変速に影響する半径方向の力に関係しないことになります。
言い換えると、隣り合うチェーンのコマからの影響は一切無視できます。
この仮定を示したのが下の図です。
半径方向に働く力
さて、チェーンのコマに働く円周方向の力は、半径方向の力に影響を与えないことがわかりました。
次に、半径方向の力について考えていきます。
半径方向の力の存在によって、チェーンを構成するコマはプーリーの半径方向に移動することができ、巻きかけ径が変化し、変速できることになります。
つまり、リニアトロニックにおいて最も考慮するべき力であることがわかりますね。
この半径方向の力については、プーリーがチェーンを挟み込む力で生み出されるものです。
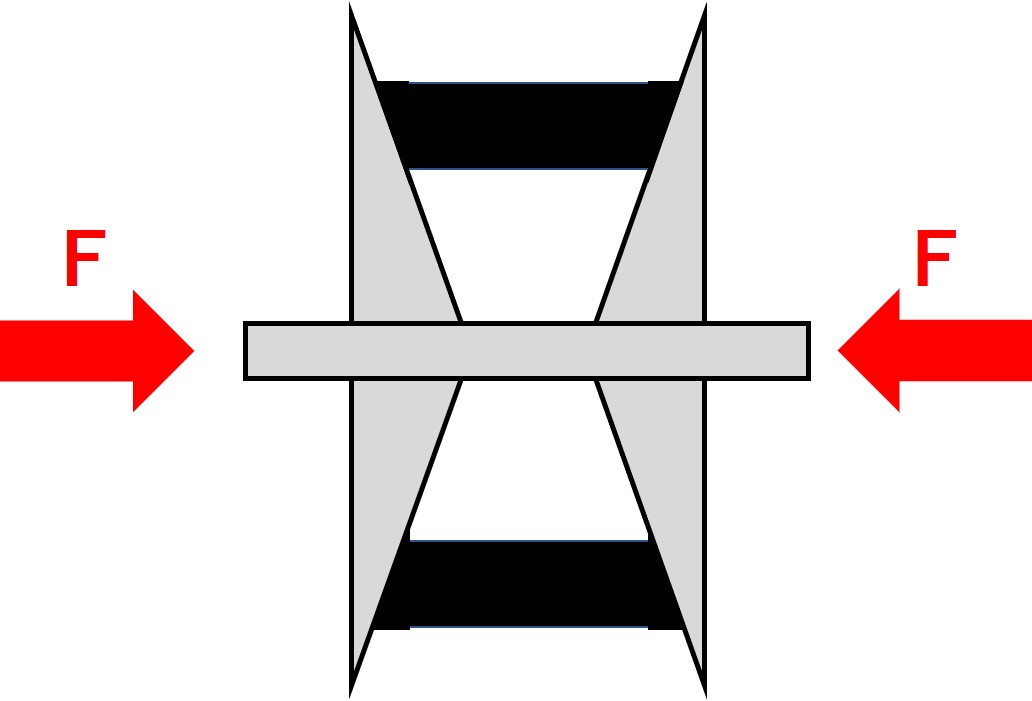
この状態について、詳細な力の関係を見ると、下の図のようになっています。

挟み込む力をFとして、成分分解を行います。
まず、挟み込むために使う力Fは、チェーンのコマとプーリーの接触面を境界とすれば、図中の$F^{\prime}$と表すことができます。
Fと$F^{\prime}$は、CVTに対して固有の線形関係があるものです。
しっかりと成分分解をすると、次の関係式が成り立ちます。
$$F^{\prime}=Fcos\Theta$$
※この点については本質的な部分ではないので詳細の説明は割愛します。
次に、チェーンのコマに働く力を考えます。
成分分解すると、上の図にあるように、2つの力に分解できることがわかります。
ここで、半径方向の力として残るのは、$F^{\prime}sin\Theta$の部分だけとなります。
この力が、巻きかけ径を変化させ、変速を行うために重要な力となります。
CVTにおける変速とは?
さて、半径方向の力が判明したことで、もう一つの力を考えましょう。
先ほど考えた、プーリーがチェーンを挟み込む力によるチェーンのコマへの半径方向に力だけでは、CVTの変速の擁する説明することができません。
なぜなら、挟み込む力だけしか考慮しなければ、巻きかけ径を大きくすることしかできないからです。
では、巻きかけ径を小さくするための力はどこからくるか?
それは、チェーンの全長は一定であることに由来します。
つまり、反対側のプーリーの巻きかけ径が大きくなることで、その巻きかけ径の変化に合わせて反対側の巻きかけ径が変化する。
この状態を図で表現しました。
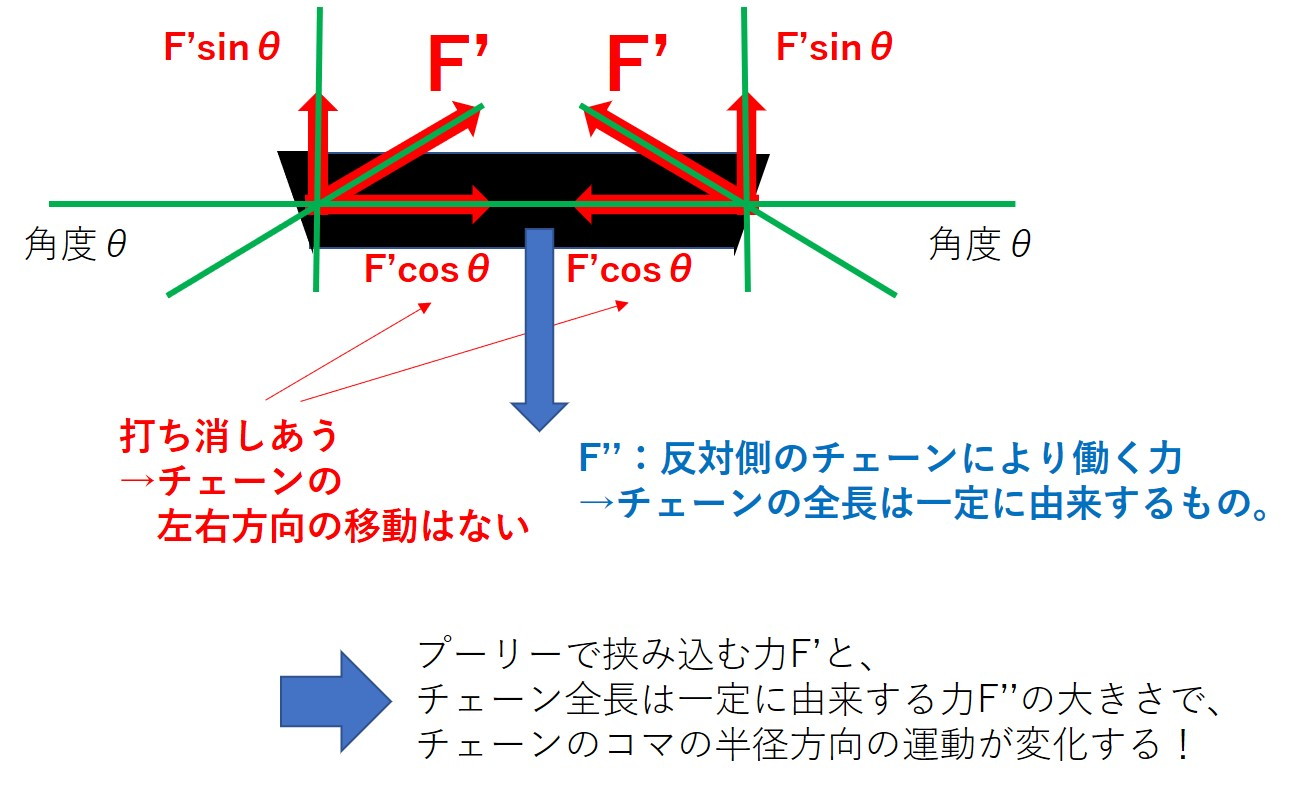
例えば、入力側のプーリーの巻きかけ径が小さく、出力側のプーリーの巻きかけ径が大きい場合(この状態がLow)、入力側プーリーの巻きかけ径を少し大きくしたときに、出力側プーリーの巻きかけ径が小さくなといった動きをします。
言い換えるなら、入力プーリーと、出力プーリーの挟み込む力が、互いに干渉していることになります。
この力は不明なので、ある力$F^{\prime\prime}$とでもしておきましょう。
これで、リニアトロニックの変速状態を考慮するための下準備が整いました。
変速における摩擦力との力の依存関係
先ほど考えていた、チェーンを構成するコマに働く力の図を見てみます。

この図において、チェーンを挟み込む力$F$によって、チェーンの半径方向の力が変化し、変速ができると書きました。
しかし、よく考えてみると、リニアトロニックはチェーンとプーリーの摩擦力により伝達しています。
実は、この摩擦力は、挟み込む力$F$の大きさに依存します。
チェーンのコマとプーリーの境界平面の法線方向に働く力は、上の図より$F^{\prime}$となります。
ここで、片側のプーリーのチェーンの巻きかけ径全体の接触面積$S$とします。
すると、力$F$で挟み込んだプーリーにおけるチェーンのコマへの圧力は、単純に面積で割ればいいので、$\frac{F^{\prime}}{S}$となります。
チェーンのコマ1つ分の接触面積を$dS$とすると、コマ一つ当たりの力で見れば、プーリーとの接触面において垂直に働く力は、$\frac{F^{\prime}}{S}dS$となります。
チェーンとプーリーにおける最大静摩擦係数路$\mu$とすれば、コマ一つ当たりに働く最大の静摩擦力は、$\mu \frac{F^{\prime}}{S}dS$となります。
チェーンとプーリーの接触面積が全体でSであり、コマ一つ当たりの接触面積が$ds$であるので、プーリーと接触しているコマの数は、$\frac{S}{dS}$個です。
したがって、プーリーとチェーンの間に働く摩擦力は、次の関係で示されます。
$$\mu \frac{F^{\prime}}{S}dS \frac{S}{dS}=\mu F^{\prime}$$
これで、変速時に重要となる力Fは、プーリーとチェーンにおける摩擦力にも影響することがわかりました。

CVTの変速中は伝達効率が変化する
以上より、変速においてプーリーを挟み込む力が変化すれば、プーリーとチェーンの間に働く摩擦力も変化することがわかりました。
摩擦力は、滑る寸前が一番強いです。
これを最大静摩擦力というのですが、身近な例でいうと、車でABSがありますね。
ブレーキを踏んでタイヤがロックすると、タイヤと路面の摩擦力が静摩擦から動摩擦へ変化することで、制動距離が伸びます。
これを防ぐために、タイヤと路面の摩擦力が最大静摩擦力になるように制御しているのが、車におけるABSです。

CVTの話に戻しますと、挟み込む力が強くなれば、チェーンの巻きかけ径が大きくなる方向に力が作用すると同時に、プーリーとチェーンの間の摩擦力も大きくなります。
逆に、挟み込む力を弱くすれば、チェーンは巻きかけ径が小さくなる方向に力が作用しますが、プーリーとチェーンの間の最大静摩擦も小さくなり、伝達できる駆動力が小さくなります。
したがって、CVTの変速中は、こういった複雑な要素が絡み合っていることになります。
変速するには、次の2パターンが考えられます。
1.一方のプーリーの力を弱める
一番簡単なのがこの方法です。
巻きかけ径を小さくしたい法のプーリーの挟み込む力を小さくすれば、巻きかけ径を大きくしたい法のプーリーの力が相対的に強くなり、チェーンの全長が一定の条件から、CVTとしての変速が可能になります。
しかし、先ほどにも書いたように、プーリーとチェーンの間の摩擦量の低下から、伝達できる最大の駆動力が著しく低下します。
もしもプーリーとチェーンの間の最大静摩擦力を越える駆動力が入力されると、プーリーとチェンの間が滑ってしまい、大幅なロスになります。
すなわち、エンジン出力に制限ができることになります。
2.一方のプーリーの力を強める
摩擦力の低下によるエンジン出力の制限を考えるなら、巻きかけ径を大きくしたいプーリーの力を強めて、相対的な力の差で無理やり変速する方法もあります。
この場合には、おおきなちからでプーリーを挟み込む際に必要となる油圧のロスが生じます。
さらに、強力な力でチェーンを挟み込むことによる、チェーン及びプーリーへの耐久性の問題もあります。
これらの状況より、変速中においては効率の低下などの問題が生じます。
よって、フルスロットル時には、無段階変速をすること自体があまり得策ではないため、スバルのS#モードでは、8段ステップ制御が行われているといえます。
8段ステップ制御を使えば、固定ギア比の時にはエンジンパワーをフルに伝達でき、逆に変速する瞬間にはエンジン出力をいったん抜いて、素早く変速した後再びエンジン出力を入力すれば、CVTとしての変速中のネガティブな要因を消すことができ、300馬力のエンジンがフルパワーで加速できることになります。

レヴォーグにおける裏モード加速
最後に余談ですが、レヴォーグにおける裏モード加速を考えます。

レヴォーグの2.0Lモデルには、裏モードというものがあります。
S#モードで停車中にブレーキを踏んだ状態でアクセルを踏み込みます。
そのままブレーキを話して加速すると、ローンチコントロールになり、フル加速できるモードです。
この時、リニアトロニックは無段階変速が行われており、この記事の内容だけでは説明しきれない部分が生じてしまうのです。
ここについても考えていきましょう。
無段階変速を行う裏モードとSモードの変速を見ていきます。
1.6Lモデルと2.0Lモデルの違いはありますが、変速の挙動において、その差は一目瞭然でした。
※今後2.0LモデルのレヴォーグのSモード加速が見つかれば差し替えます。
レヴォーグ 1.6LのSモード加速。
レヴォーグ 2.0Lの裏モード加速。
同じ無段階変速をしているとはいえ、Sモードでは、最高出力発生回転数付近でなめらかに回転数変化を抑えています。
これは、最高出力を発揮する前から変速を行っていることになり、最速で最高出力までエンジン回転数を変化させていません。
一方、裏モード加速の場合には、一気に5600rpmまで回してから、そのまま回転数を維持しています。
イメージで見ると、次のようなグラフになります。
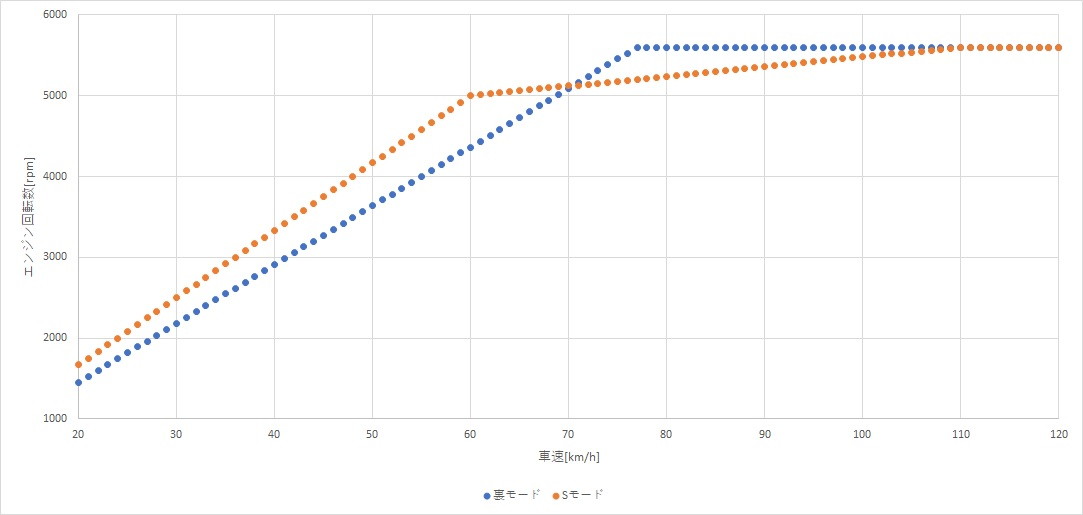
ここで、裏モード加速において、5600rpmを維持する瞬間のチェーンに加わる力を考えます。
レヴォーグのスペックから、1速の時の減速比はわかるので、タイヤ回転数の増加とともに変速が行われる様子をプロットしました。
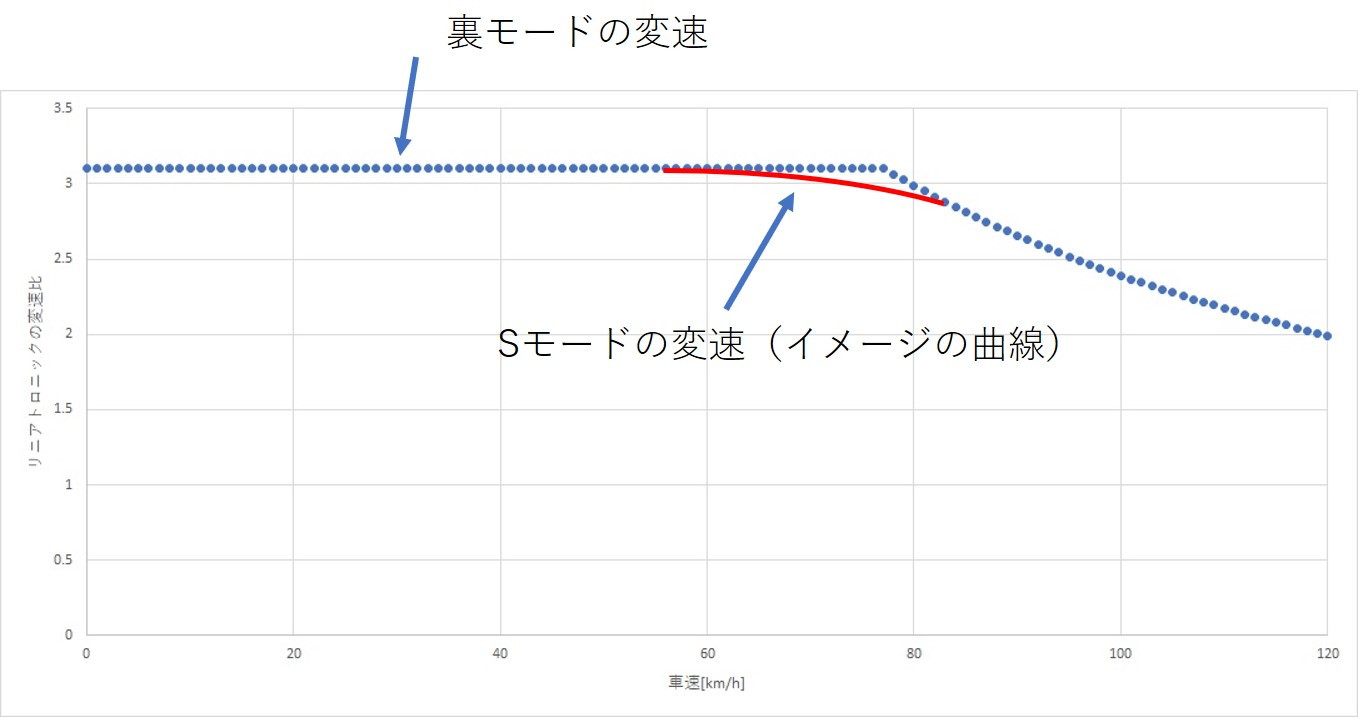
この図からわかるように、急激に5600rpmに上昇させて、その回転数を維持する瞬間に、滑らかではない変速が行われます。
また、300馬力をフルに発揮している瞬間であると考えると、先ほどの変速の様子から察するに、挟む力を強めることで変速を行っていることがうかがえます。
この時に油圧による効率の低下が考えられますが、ローンチコントロールにおいては、ブレーキとアクセルを同時に踏んでいる時間があるので、この時に無駄になるエネルギーを使えば、加速中の効率については何かしらの対策ができそうです。
※だから、停車時のみ裏モードにすることができ、走行中に裏モードにすることはできないのでしょう。
例えば、発進前に油圧を十分に高めておくことなどが考えられます。
恐らく、オーバーブースト機能とは異なる仕組みです。
それ以上に問題となるのは、リニアトロニックの負荷の影響でしょう。
よって、ローンチコントロールで加速する数十秒間は、効率面では何らかの対策ができたとしても、リニアトロニックへの負荷は相当なものになるでしょう。
あえて裏モードとして、日常的には利用できないように制限しているのも、リニアトロニックの耐久性の問題からではないかと予想できます。
結論としては、レヴォーグの裏モード加速は、その場一瞬の加速を見るだけなら優れていますが、油圧ロスに関しては何らかの特殊な制御があるだろうし、リニアトロニックの耐久性の問題も含めると、日常走行においてマトモに多用できるシステムであ有りません。
よって、特殊な制御を一切なしにすれば、やはりリニアトロニックをステップ制御するのが一番得策といえます。
まとめ
ここまで、スバルのリニアトロニックが、S#モード時に8段ステップ変速を行う理由について考えてきました。

CVTでは、変速において用いる挟み込む力は、プーリーとチェーンの間の最大静摩擦力にも影響してきます。
よって、変速を行う場合には、巻きかけ径を小さくする側のプーリーの挟む力を小さくすれば、エンジン出力の伝達において制限が生じ、逆に巻きかけ径を大きくする側のプーリーの挟む力を大きくすれば、油圧においてロスが生じ、効率が低下します。
したがって、一定ギア比で加速し、変速の瞬間だけエンジン出力を抜いて素早く変速したほうが、総合的な加速性能では上回ることを考えてきました。
無段階変速を行ったまま加速するレヴォーグの裏モードのに関しては、特殊な条件が重なったときの例外的な性能であって、変速中の効率に関しては、何かしらの特殊な制御が行われているでしょう。
また、リニアトロニックの耐久性の面からも、常用的に使える機能ではありません。
以上、スバルのS#モードが、8段ステップ制御を行う理由について、参考になれば幸いです。
以下の記事で、WRX STIにFA20″DIT”が搭載されない理由を考えました。
FA20″DIT”は、リニアトロニックと組み合わせることで最高のパフォーマンスができるエンジンになっています。
リニアトロニックの伝達効率と、エンジン単体の効率、この掛け合わせでトレードオフの関係になっています。